top of page
Search

Alpha Divergence

  • Writer: Rana Basheer
    Rana Basheer
  • Apr 21, 2011
  • 1 min read

Updated: Apr 2, 2021

On several occasions you want to classify an observation x into one of two categories









Depending on which ever probability is higher we classify x as either being in



However, there is a non-zero probability that x might belong to




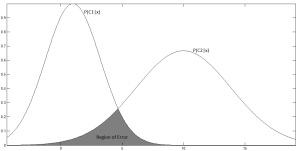
Bayes Error


Larger the area under this region there is a greater chance for misclassification. The area under this error region is given by


A=\int{min\left(P\left(C_1|x)\right),P\left(C_2|x\right)\right)p(x) dx}

Since minimum function is quite difficult to deal with it is replaced by a smooth power function as

min\left(a,b\right)\le a^\alpha b^{1-\alpha},\forall \alpha \in \left(0,1\right)

Hence the upper bound for the area is given by


A \le \int P\left(C_1|x\right)^\alpha P\left(C_2|x\right)^{1-\alpha} p(x) dx =P\left(C_1\right)^\alpha P\left(C_2\right)^{1-\alpha}C_\alpha \left(P\left(x|C_1\right)||P\left(x|C_2\right)\right) dx

C_\alpha \left(P\left(x|C_1\right)||P\left(x|C_2\right)\right)=\int P\left(x|C_1\right)^\alpha P\left(x|C_2\right)^{1-\alpha}


The


D_\alpha=-log\left(C_\alpha\left(\cdot||\cdot\right)\right)

Comments

bottom of page